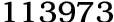|
Introduction to negative exponents algebra: In mathematics negative exponents algebra is very simple topic. In algebra exponents are called as powers. Algebra exponents are very important part of mathematics. Exponents are denoted that a number is multiplied by same number for a given several times. The exponent of a number is says how many times to use the copy of the number in a multiplication. Negative exponent is dividing the inverse of multiplying. Example: 2-3 = `1/2^3` =`1/8` `(1/6)^-1` = 6. Laws of Negative Exponents Algebra: a-n =`1/a^n` a-n is reciprocal of an `1/a^-n` =an `1/a^-n` is same as an Rules for exponents: x1 = x x0 = 1 xmxn = xm+n `x^m/x^n` = xm-n (xm)n = xmn (xy)n = xnyn (x÷y)n = xn ÷yn Suppose x would be zero, x= 0 what we do? Positive Exponent algebra means (n>0) 0n = 0 Negative Exponents algebra means (n<0) Solution is Undefined! (Because dividing by 0) Negative exponent of a number is the reciprocal of that power with a positive exponent. A negative exponent algebra means divide, because the opposite of multiple is divide. Practice Problems - Negative Exponents Algebra: Example 1: Simplifying Fractions with negative exponents algebra: To raise a fraction power, increase the numerator and denominator to that power. `(x^-3y^-4)/y^-2` =`x^-3y^-4y^2` Answer is = x-3y-2 Example 2: Simplify negative exponents algebra `7^4/7^-3` Note : answer would be positive exponents. Solution: `7^4/7^-3` =7473 Now add like terms power `7^7` =823543 (answer) Example 3: Simplify negative exponents algebra. The answer only in positive exponents (7a-4b2c0)-4 Solution: Given expression is (7a-4b2c0)-4 (7a-4b2c0)-4 = `1/((7a^-4b^2c^0))^4` =`1/(7^4a^-(16)b^8c^0)` =`1/(2401a^-(16)b^8)` = `(a^16)/(2401b^8)` Example 4: Rewrite without a denominator:`a^2/(a^-1b^-4c^-2)` Solution: Given expression is :`a^2/(a^-1b^-4c^-2)` = a2ab4c2 =a2+1b4c2 =a3b4c2 Example 5: Simplify negative exponents algebra. The answer only in positive exponents `(x^-2y^-3)/(xy)` Solution: Given expression is `(x^-2y^-3)/(xy)` = `1/(xyx^2y^3)` = `1/(x^(1+2)y^(1+3))` = `1/(x^3y^4)`(Answer) Know more Rules for Exponents i found this interesting link Exponents Rules
Related Articles -
Negative, Exponents, Algebra,
|